FFT – Fast Fourier Transform
Oggi voglio parlarti della FFT, acronimo di Fast Fourier Transform. In questo post approfondiremo cos’è la FFT, come funziona e perché è una delle tecniche più potenti e usate in elettronica e nel trattamento dei segnali digitali. Ti spiegherò tutto con esempi tecnici e pratici così da farti capire come applicarla nei tuoi progetti.
Cos’è la FFT?
La FFT è un algoritmo efficiente che calcola la Trasformata di Fourier Discreta (DFT) di un segnale. In parole semplici, prende un segnale nel dominio del tempo — ad esempio un suono registrato — e lo trasforma nel dominio delle frequenze, permettendoci di vedere quali componenti frequenziali sono presenti e in che misura.
Fft (fast fourier transform, analisi fft, fft fft, fast fourier)
Prima dell’avvento della FFT, la DFT richiedeva molti calcoli, il che la rendeva poco pratica per segnali lunghi o in tempo reale. La FFT riduce drasticamente la quantità di calcoli necessari, rendendo possibile l’elaborazione veloce anche su dispositivi con risorse limitate.
Come funziona la FFT?
La FFT sfrutta una proprietà matematica chiamata “divide et impera”. In pratica, scompone la DFT di un segnale lungo N in due DFT più piccole da N/2 elementi ciascuna, e ripete questo processo fino ad arrivare a DFT elementari di dimensione 1. Questo metodo riduce la complessità da O(N²) a O(N log N), un enorme risparmio computazionale.
Esempio tecnico: analisi di un segnale audio con FFT
Immagina di avere un segnale audio campionato a 8 kHz per 1 secondo, quindi 8000 campioni. Se vuoi sapere quali frequenze sono presenti in questo segnale, devi calcolare la sua trasformata di Fourier.
- Applichi la FFT ai 8000 campioni.
- Ottieni un vettore di 8000 valori complessi che rappresentano ampiezza e fase delle frequenze da 0 a 4 kHz (la metà della frequenza di campionamento, nota come frequenza di Nyquist).
- Puoi calcolare il modulo di questi valori per ottenere lo spettro di ampiezza delle frequenze.
Grazie alla FFT, questo processo richiede pochi millisecondi su un microcontrollore moderno, mentre con la DFT classica sarebbe stato quasi impossibile farlo in tempo reale.
Applicazioni pratiche della FFT
- Analisi spettrale: identifica le frequenze dominanti in segnali audio, vibrazioni meccaniche o segnali RF.
- Filtraggio digitale: puoi trasformare il segnale, eliminare o attenuare certe frequenze e poi tornare al dominio del tempo con la trasformata inversa (IFFT).
- Compressione audio e immagini: algoritmi come MP3 o JPEG usano trasformate di Fourier per ridurre la quantità di dati.
- Diagnostica medica: analisi di segnali ECG o EEG per identificare anomalie nel dominio delle frequenze.
Dettagli tecnici importanti
La FFT richiede che il numero di campioni sia una potenza di due (es. 256, 512, 1024). Se il tuo segnale ha un numero diverso di campioni, devi eseguire un processo chiamato “zero padding” per adattarlo.
Un’altra cosa da tenere presente è la risoluzione in frequenza: maggiore è il numero di campioni, migliore sarà la risoluzione, cioè la capacità di distinguere due frequenze vicine. Questo però richiede più memoria e potenza di calcolo.
Un rapido esempio matematico
Per darti un’idea, la formula della DFT per un segnale x[n] di N campioni è:
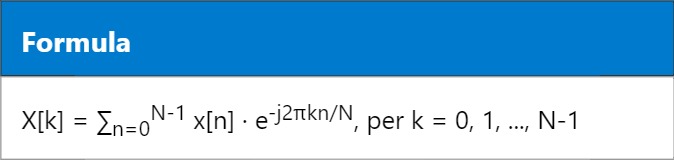
Dove X[k] è il valore complesso della frequenza k-esima. La FFT calcola questi valori senza dover ripetere tutte le moltiplicazioni una ad una, ma dividendo il problema in sottoproblemi più piccoli.
Ti dico che imparare ad usare la FFT apre davvero molte porte in elettronica e ingegneria dei segnali. Se hai mai lavorato con microcontrollori o DSP, conoscere la FFT è quasi un must per analizzare e manipolare segnali efficacemente.
Domani esploreremo il tema della Filtro Digitale FIR e vedremo come si possono usare le FFT per progettare filtri veloci e precisi, molto utili nel trattamento digitale dei segnali. Non perdertelo!